こんな授業があったんだ│第10回│算数の授業づくりの急所中の急所〈前編〉│岡田 進

算数の授業づくりの急所中の急所
タイルのゲームで10進法と位どりを教えよう〈前編〉
岡田 進
(1981年・小学1年生)
タイルのゲームで10進法と位どりを教えよう〈前編〉
岡田 進
(1981年・小学1年生)
算数の不得意な子を教えてきて
──急所中の急所とは
早いもので、わたしが学校の教師をやめて、もう2年の月日がたちます。そのあいだ、算数塾をやりながら、一方では、算数の診断・治療教室を『ひと』の誌面でよびかけ、算数の不得手な子や算数にコンプレックスをもっている子を指導してきました。
少人数の、しかも、算数ぎらいや算数に自信のもてない子どもたち相手の授業ですから、40人の子ども相手の授業とはかなりちがいます。当然、教え方も変わってきます。教師実験をやって、黒板にチョークで説明し、あとはドリルで反復練習といった、多くの学校でやられているような授業ではアクビの連発で、ソッポを向かれてしまいます。
その子たちに「なるほど、そうか」と納得のいく理解をさせ、「やってみようか」と前向きの気持ちにさせるには、頭だけではなく、手足はもちろん、からだの感覚をフルに使って、からだごとわからせて覚えさせるような授業が必要です。それも、ゲームや遊びのなかに、学習を盛りこんだような楽しい授業をすることが望ましいわけです。
わたしが子どものころ、冬の街を、「玄米パンのホヤ、ホヤー。子どもがたべたら、カアちゃんまでウマイ。カアちゃんがたべたら、トウちゃんまでウマイ」といって屋台を引いて通るパン屋がいました。でも、子どもがたべて、カアちゃんがうまいわけはなく、カアちゃんがたべて、トウちゃんがうまいわけがないように、先生が実験してよくわかっても、それを見ている子どもによくわかるかどうかは疑問です。
わたしはかねがね、何かを学習して身につけるには、実際に自分自身でやってみることがいちばんで、見たり聞いたりしただけでは「なるほど、そうだ」と納得できるようなわかり方はむずかしいと考えています。100回の説明を聞くより、1回の経験のほうが実際の機微にふれることもあって、心に残るわかり方をするものです。なにからなにまで実験させることはできませんが、できるだけ多く子どもにやらせることがたいせつだと思います。ことに小学生の場合は実際の経験をだいじにして、からだを使って理解させることが必要だと思います。
実際に手足・からだを使った学習をやらせると、口でペラペラ説明する授業とはちがってテンポがおそくなりますから、子どもも教師も間がとれます。そして、具体にそくして考えられるので、わかりやすく、落ちこぼしもグッと減少するものです。
ところで、算数は、理科や社会のように、一度、理解したら反復練習は不必要というぐあいにはいかず、計算のように、何回も何回も練習してスラスラできるようにしておかないと、やり方だけわかっていても役にたたないといった側面があります。
そこで、普通、学校ではドリル帳とかワークブックとかを与えて、宿題、宿題で追いまくっていますが、これでは子どもに敬遠されてもしかたないでしょう。ちょっとした工夫をして、ゲームや遊びのなかで練習させれば、子どもは喜んでやるものです。それで学力がつけば、これにこしたことはありません。まさに一石二鳥というものです。
このような学習のやり方は、理解のおそい子や落ちこぼされた子たちだけに有効であるだけでなく、じつは、理解の早い子、いわゆる“よくできる子”にもたいせつなものです。
頭のさきっちょだけで観念的にわかるのとちがって、具体をとおして、からだで経験してわかりますから、どうしてそうなのか、意味や内容の理解も具体的で、実際にそくしているので、応用力がつくというものです。
以上のような考えのもとに行なった実践の例を、つぎに述べることにします。学校で算数の授業をつくるとき、家庭でお子様に教えるときの参考にしていただければさいわいです。
目かくししてタイルをさわる
──9までの数の指導
わたしの塾には3人の1年生がいます。1人は4月から、あとの2人は7月から入会した子どもです。いま(1981年12月末現在)、2位数のたし算をやっていますが、1位数のくりあがりのあるたし算や、その逆のくりさがりのあるひき算などはスラスラできます。2、3年生の子といっしょにゲームをやっても、それらの計算ではあまり負けなくなりました。だから、この子たちは算数が得意で、ゲームが大好きです。
ところで、この子たちも最初から算数が得意であったわけではありません。
7月に入会した2人の場合など、3+2の計算をやらせたら、A君は机のうえで両手を開いて、指を3本と2本のばして、それを1、2、3、4、5と数えて答えを求め、B君は指を1、2、3と数えて折って、それに1、2と折りたして、折った指の数をかぞえて答えの5を求めていました。
7-4というひき算では、A君は7本の指を開いて、そのうち4本を1、2、3、4とくちびるにあてて折りまげて残りの3を求め、B君も開いた7本の指のうち4本を、1、2、3、4と折りまげて答えの3を求めていました。2人とも指を使って「数えたし」「数えひき」の計算をしているのでした。
そこで、指を使わないように指示して計算させたところ、どちらの子も困った様子で、答えを求めるのに四苦八苦、たし算は目を白黒させながらも数えたしでなんとかできましたが、ひき算はお手上げでした。
指を使って数えたしたり、数えひいたりすれば、10までの数とそのたし算・ひき算は、だいたい100点か、それに近い点がとれます。ところが、10より大きい数の計算になると、そうはいきません。手の指が10本しかないので苦労します。数えることをできるようにすることも必要ですが、数えることを中心にした数え方だと、数の大きさを意識してとらえなくても不自由しないせいか、数の大きさを1つのかたまりにまとめてとらえるのがおろそかになって、計算に弱くなります。
くりあがりやくりさがりのあるたし算・ひき算でつまずく子の多くは、1位数の大きさをはっきりとらえていないのです。
算用数字は、1を10コ束にして10、10を10コ束にして100というように、10コずつ束にしていく仕組み、いわゆる十進法と、それに位取りの原理を組みあわせて、どんな大きな数でもあらわせる仕組みになっています。その仕組みを使って加減乗除の計算をするのです。ですから、算数・数学のいちばんの基礎は、
① 1ケタの数字(0、1、2……9)の大きさをひと目で、しかも、イメージ化できるほど、しっかりとらえさせること。
② 十進位取り記数法の仕組みをよく理解させること。
この2つは、小学校の算数の急所中の急所ということになります。
ところが、教科書では、9までの数をひと目でとらえさせたり、イメージ化してとらえさせたりするようなあつかい方はしていません。位取りの指導も、3~4ページでかんたんに処理し、計算棒や丸、おはじきなどの教具を使ってお茶をにごしています。
9までの数の大きさもはっきりせず、位取りもあいまいなまま計算させたら、子どもがよくわからないで苦労するのは、火を見るよりあきらかです。くりあがりのあるたし算やくりさがりのあるひき算、2、3位数のたし算・ひき算など(とくにひき算)で子どもがつまずくのは、そこにひとつの原因があるように思います。
1年生の算数の第1のポイントは、9までの数をひと目みただけでとらえられるようにし、その数の大きさを大脳に焼きつけることです。これができると、つぎのポイントである、9までの数を並べて数の大きさを表現する位取りの原理もわかりやすくなります。
ところで、9までの数をひと目でとらえさせるには、5の「かんづめタイル」を使用するのがコツです。バラのタイルを1コずつ並べたのでは、9コのものを直感でとらえることはできません。
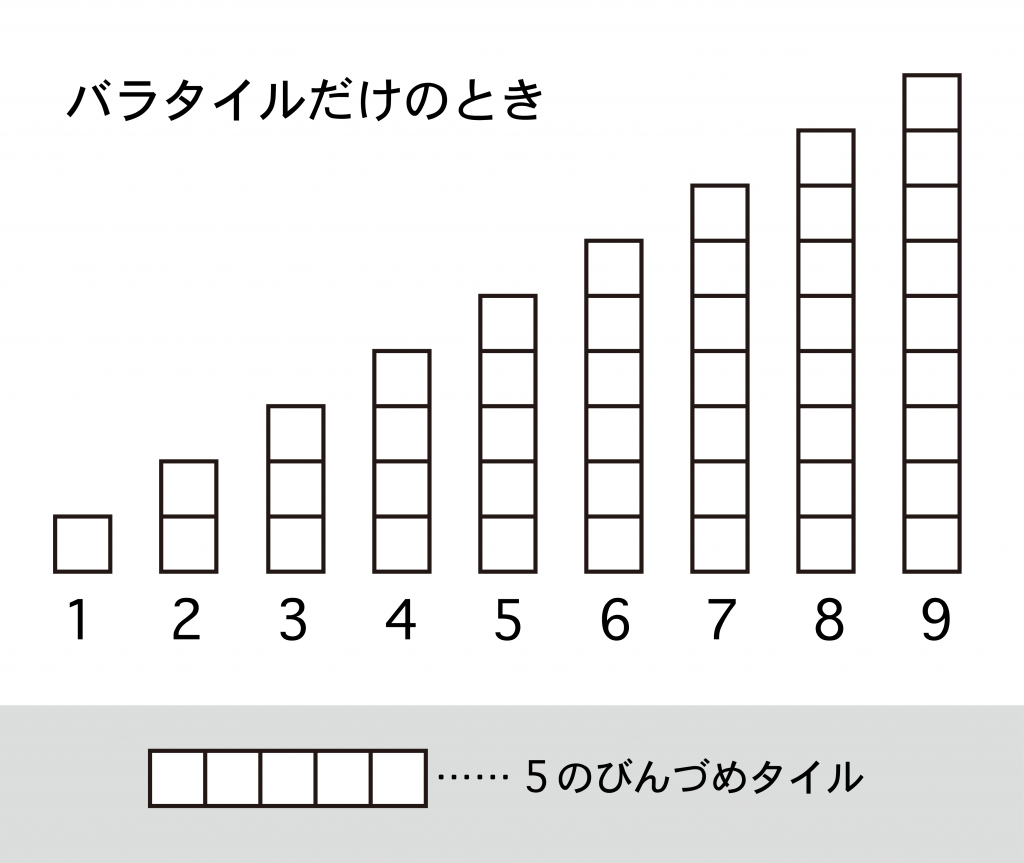
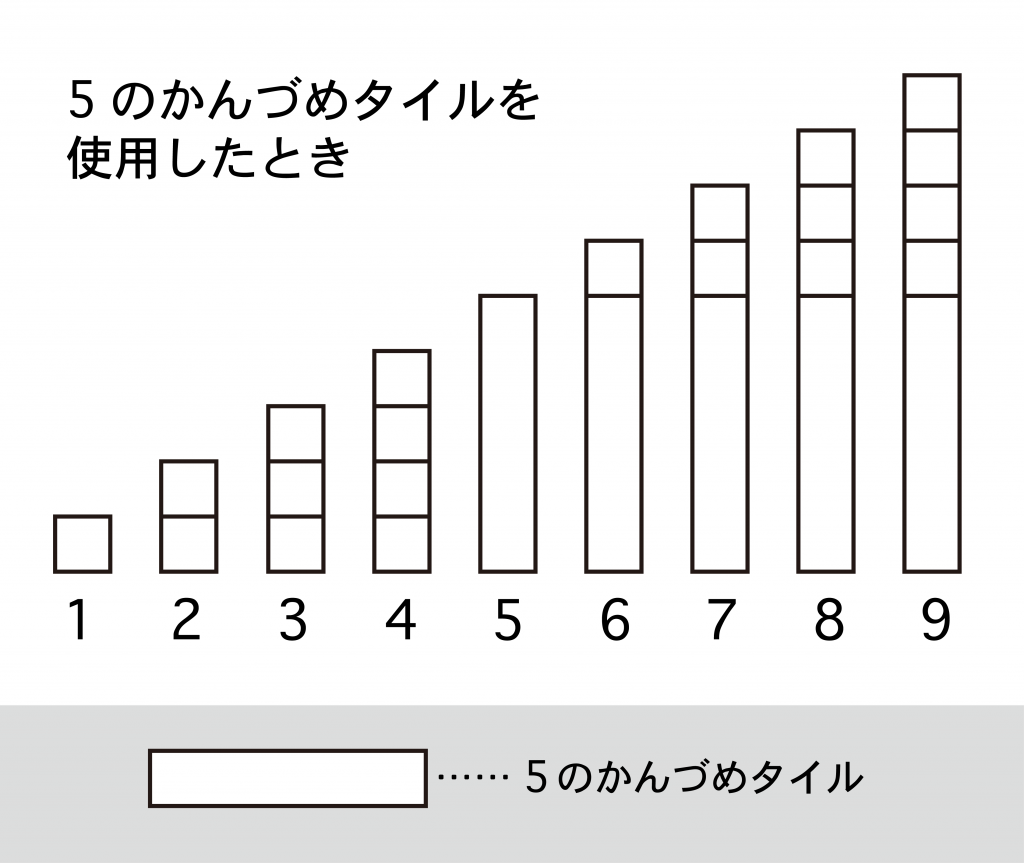
では、5のかんづめタイルを使用すると、すぐに9までの数が身につくかというと、これも、そうかんたんにはいきません。たしかに、
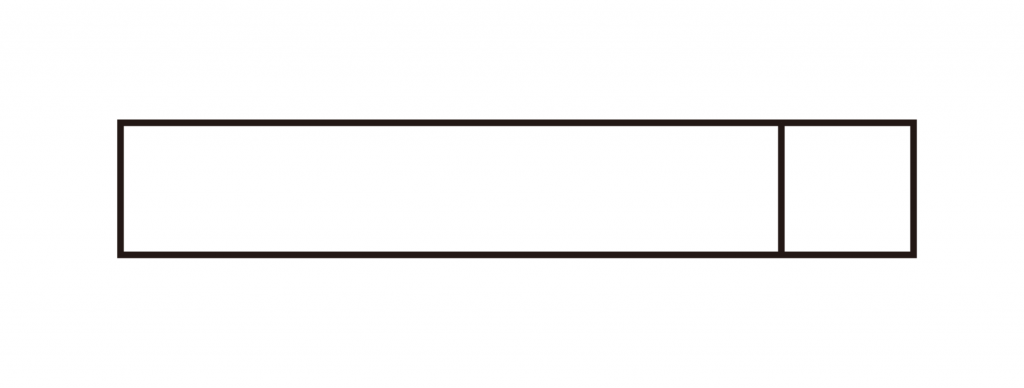
のタイルを見せると、すぐに<ろく>と答え、
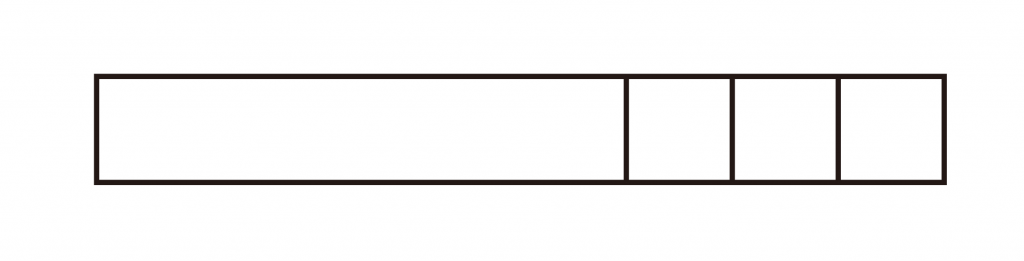
のタイルを見せると、<はち>と答えるようにはなります。
しかし、<はち>のタイルを思い出そうとしたとき、8のタイルのシェーマ(映像)がすぐに頭に浮かぶかというと、そううまくはいかないようです。

1年生のA君などは、5のかんづめタイルを使用して、9までのタイルをひと目でとらえるようになってからも、しばらくは5のかんづめタイルの表面を指で1、2、3、4、5と数えて、数えたしたり、数えひいたりしていました。数えることを中心にした算数をやってきていたので、数えてたしかめないと、なんだか不安だったのでしょう。
そこで、9までの数のタイルのシェーマを脳裏にはっきりやきつけるため、いろいろなことをさせました。そのなかで、「これはおもしろい」と思ったのが、「見えないメガネ」をかけてタイルを拾わせたり、タイルの計算をさせたりする遊びです。
これはかなりの手ごたえがあり、また、予想もしないことがわかったので、紹介することにします。
目の見えない人は点字の本を読みますが、紙面につけたチョットした凹凸の点字を読みとっていく指さきの感覚の鋭敏さには驚くばかりです。このすばらしい触覚の力を学習に使わない手はないでしょう。
かなりまえのことですが、テレビで寺尾聡が例の黒いメガネをかけて「ルビーの指環」を歌っているのを見て、「見えないメガネ」をかけさせて、触覚をたよりに手さぐりのタイルとりをやらせたら、おもしろいだろうなと思ったのです。そこで、さっそく白ボール紙でメガネをつくり、それをマジックで黒くぬって、つぎのような遊びをしました。
……………………………………
●目かくしタイルとりゲーム
<準備>
*1㎤(1㎝×1㎝×1㎝)のプラスチック製の立方体(通称、みつ豆タイル)100コ。5のかんづめタイル(1㎝×1㎝×5㎝)10コ。この2種類のタイルを小箱に入れて、ゲームをやる子のまえに1箱ずつおく。
*「見えないメガネ」。白ボールまたは厚手の紙でつくる。1人に1コずつ持たせる。なお、メガネのかわりに、「見えないお面」にして、「ガンダム」「ドラえもん」などをつくらせてもよい。
*数字カード0、1、2……9を1組、または、下図のような正十二面体のサイコロを1コずつ準備する。

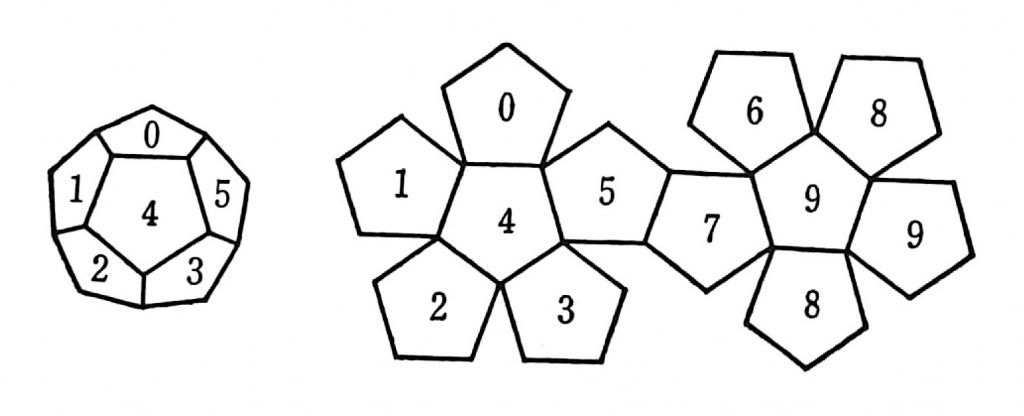
<ゲームのやり方>……絵①
*机のうえにみつ豆タイルのはいった小箱をおき、とり手には「見えないメガネ」をかけさせる。
*読み手は数字カードのなかから1枚とって、数字を読み、その数のタイルを、とり手に手さぐりで小箱のなかからとらせ、箱の外に置かせる。読み手は2回(または3回)ずつで交替する。
*読み手は1回ごとに○×を表につける。途中でメガネをはずしたり、メガネをずらしてのぞき見したりした子には×、とったタイルの数がちがっている子にも×、タイルの数があっている子には○をつける。
*全員が読み手を2回(または3回)ずつやったら、ゲームをやめる。
*○が多い順に1等、2等……とする。

このゲームは、手さぐりで触覚をたよりに指示された数のタイルを箱のなかから拾うのですが、どの子もほとんどまちがえずにできるのには驚きました。わたしも、そのメガネをかけてタイルとりをやったのですが、なにも見えないのに、タイルの個数だけが指さきや手のひらの触覚ではっきりとらえられたのは意外でした。これはおもしろいと思ったので、「9までの数のたし算(ひき算)の目かくしタイルとりゲーム」をやらせてみました。
……………………………………
●目かくし たし算ゲーム
<準備>
*「見えないメガネ」を各自に1コずつ。
*下図のような計算カード(0から9までのたし算)。
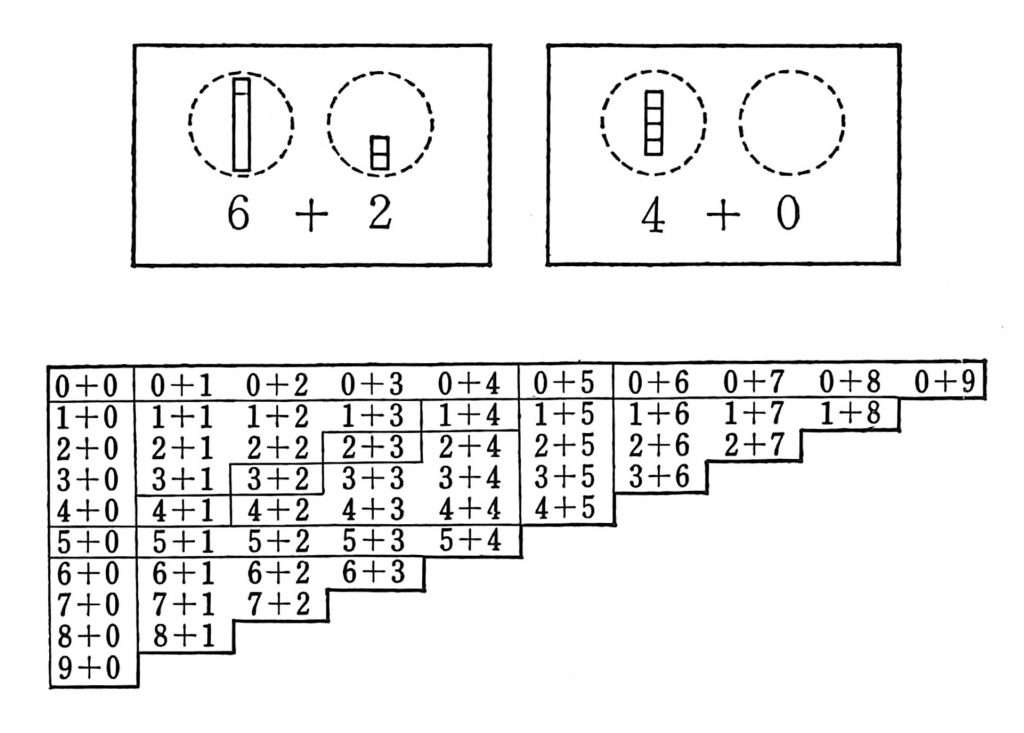
*小箱にみつ豆タイルを100コ、5のかんづめタイルを10コ入れて、ゲームをやるひとのまえにおく。
<ゲームのやり方>……絵②
*3問(または5問)ごとに読み手を交替する。読み手は計算カードのなかから1枚とって、その計算を2回くりかえして読む。「6たす2」──すこし、まをおいて──「6たす2」と。
*見えないメガネをかけたとり手は、みつ豆タイルの箱に手を入れて、手さぐりで左手に6コ(5のかんづめタイル1コとバラ1コ)、右手に2コ(または、はじめに6コ、あとから2コ)とって、それを合わせて答えを求め、「6たす2は8」と式と答えを読み手に知らせる。1対1でやる場合は声を出して知らせてもよいが、1対多数の場合は、読み手の耳元に小さい声で言うようにする。
*読み手は答えをしらべ、あっていれば、みつ豆タイル1コをとり手にあげる。
*読み手は、答えがわからないときは、タイルを並べて計算して答えをたしかめる。
*ゲームは、計算カードがなくなったとき終了。もらったタイルの多いものから1等、2等……ときめる。

[備考]ひき算についても同様のゲームをやらせたが、ひき算の場合、6-2、6-3、6-4、7-3、7-4、8-4の6題については、5のかんづめタイルをバラのタイルにくずす操作が、目が見えないのでむずかしく、これらは別にしてあとで練習させたほうがよいと思った。
* * *
目かくししてタイルのたし算・ひき算をやらせてみて、早くて正確にできるのは意外でした。そこで、目かくししない場合とくらべたところ、理解の早い2人の子はどちらもそう変わらなかったのですが、理解のおそいA君の場合は目かくししたほうが早いのです。「へんだな。そんなはずはない」と思って、2、3回やらせたのですが、やはり、目かくししたほうが早いのでした。そこで、わたしも見えないメガネをかけてやってみたところ、なにも見えないせいか、手の触覚でタイルの数だけを鮮明に感じとることができ、6+2が8になることだけに神経が集中するので、目で見ながらやるより気が散らないことがわかりました。
タイルを見せて計算させると、ふで箱やえんぴつやノートなど、見えなくていいものまで目にはいりますから、神経が集中できない子は気が散って、おそくなったり、まちがったりするのでしょう。これは意外な発見でした。子どものなかには、あたりが気になって落ちつかない子や、ひとつのことに集中できない子などいますが、そんな子には、教材によっては、この「見えないメガネ」や「見えないお面」、それに「手さぐり箱」などを使って指導すると、効果があがるのではないかと思います。
ところで、9までの数のゲームをやるには、5のかんづめタイルづくりがひとつのポイントで、5円玉や50円玉、それに、ソロバンの5珠のように、ごく自然に使えるようにすることが必要です。
わたしの塾の3人の子どもたちは、学校で9までの数とそのたし算は教わっていたので、数えることはできたし、数字の読み書きもできました。しかし、5コをまとめてとらえることは教わっていませんでしたので、5のかんづめタイルづくりは知らないわけです。
そこで、9までの数について、みつ豆タイルをひとつひとつ積みあげてタイルの階段をつくらせ、5より1大きい数が6、6より1大きい数が7……というようにして9までの数をおさえました。
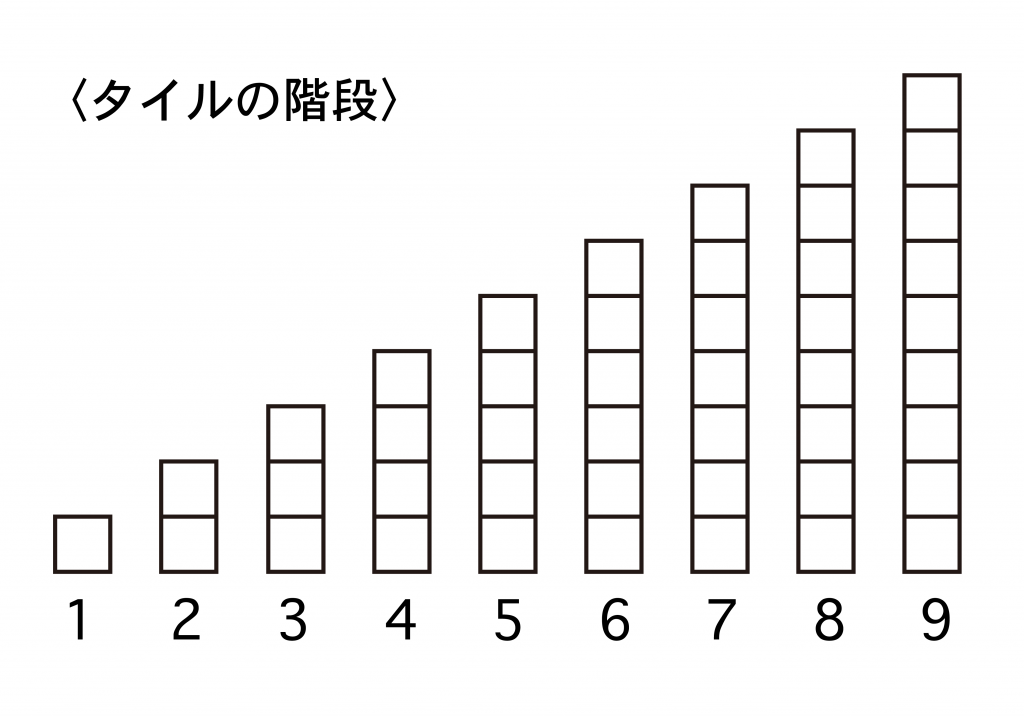
つぎに、机のうえに並べたタイルの個数をひとめ見て当てさせました。3コまではどの子もひとめで数を言いあてましたが、4コになると、ひとめ見ただけではわからない子もおり、5コ以上になると、どの子も数えて個数を答えていました。
そこで、9までの数がひとめでわかる工夫をしようということで、タイルを5コずつセロテープで巻いて5の棒タイルをつくらせ、それを使って6、7、8、9の数をあらわしました。これだと、バラのタイルを下図のようにすこし離しておくと、いくつかすぐにわかりますが、ピッタリくっつけると、1コ1コのしきりが目ざわりで、ひとめで判断できなくなります。そこで、仕切りのない棒になっている5のかんづめタイルを使用することにしました。
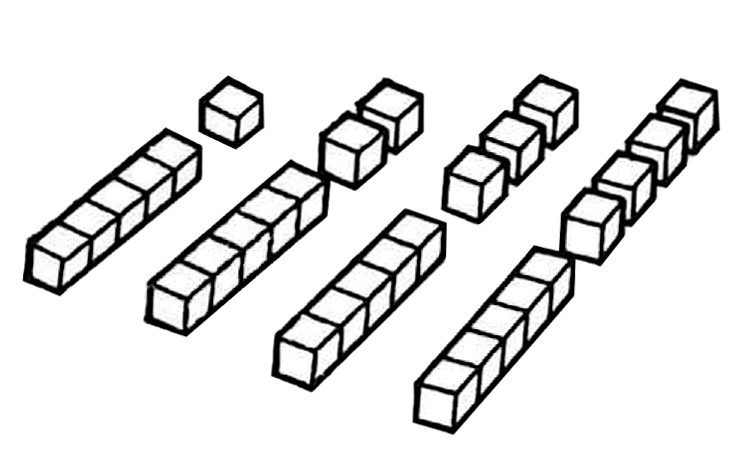
こうして、このタイルを使って9までのタイルの階段づくりをさせ、前述のタイルとりゲームをやらせたというわけです。(後編につづく)
[マンガ:佐々木ケン]
出典:『ひと』編集委員会編『ゲームの算数』、初出『ひと』1982年4月号、太郎次郎社
岡田 進 (おかだ・すすむ)
1926年生まれ。千葉県で小学校教員を経て、私塾を主宰。タイルを使ったさまざまな算数教育の実践で知られる。著書に『算数 つまずきの診断と治療』(明治図書)、『これなら楽しくできる 漢字の教え方』(太郎次郎社)、共著書・監修書に『親子で学ぶ算数教室』(日本書籍)、『らくらく算数ブック』1~3、『らくらく数学テキスト』中学1年(ともに太郎次郎社)などがある。
![[Edit-us]](https://www.editus.jp/wp-content/uploads/2021/01/c04ff33146ebacd91127e25459d47089-1.png)



