こんな授業があったんだ│第21回│99 までの数の指導│芳賀雅尋

前編を読む　（単行本では前編と本稿のあいだに「９までの数」の指導が収録されています。）

　10台の数を2位数として位置づけるべきだと考えている人でも、「20までの数」という区分のなかで学習している人が多いようです。前にも触れましたが、10台の数は2位数のなかでも特殊な読み方をする数です。十の位の1を読みません。また、一の位の0も読みません。「イチジュウレイ」とは言わないわけです（100、1000もそうですが）。
　ですから、10は2位数の体系の中の特殊形として扱う必要があると考えます。43は十の位の数を読んで「ヨンジュウ」そして一の位の数を読んで「サン」となるので、続けて言うと「ヨンジュウサン」になります。40で一の位の0は読まない約束を教えて「ヨンジュウ」、そのつながりで30、20、10と進んで、10は十の位の数を読まないで「ジュウ」ということを約束とします。そのあとに10台の数の学習をします。
　余談ですが、一の位にはいくつまで入れるのでしょうか?　9まででしょうか。9を超えたら十の位に引っ越す約束ですか?じつは一の位には何個でも、そう一億個でも入れます。それはまだ構造化しないバラの状態のときです。構造化するなかで10個集めて十のタイル1本に結集したときには一の位にはいられません。そのときはじめて十の位に引っ越すのだと思っています。

たくさんのタイルで

　では、授業ではどのようなことをしたのか具体的に説明します。

　①　200mlの牛乳パックにタイルを適当に入れておきます。あまりたくさん入れると100個を越えてしまうので、そのへんは本当に適当に。わたしは子どもに自由に入れさせましたが、100個を越えないようには配慮をしました（ここで「5と5で10」をさりげなくしたいので、5の缶詰タイルをいくつか入れておくといいかもしれません）。

牛乳パックに入っているタイルは何個でしょうか。

　②　机の上にザッとあけさせます。

　③「何個かわかったら教えてください」と、子どもたちなりの方法で数を特定させます。

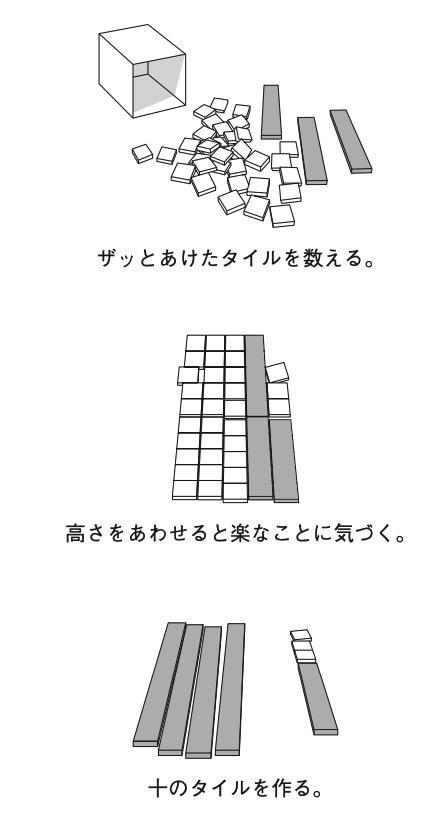
　たいていは、1から順番に数えて数を特定します。ここで、意地悪にもう一回数えさせたり、「じゃあ確かめるからね」と言って子どもとは違う数を言ってみたりします。すると、子どもは自分の数えた数に自信を失って不安になります。そこで、
「あとから見てもわかるように、全部数えなくてもわかるようにできないかな?」
と声がけをしてやります。
　すると、わたしの授業のときには、子どもたちはたくさんのバラタイルで、ガムテープを使って〝5の缶詰〟を作りはじめました。これは、5の缶詰のイメージが子どもに定着していたのか、偶然だったのかはわかりませんでしたが、「5と5でジュウのタイル（本のタイル）」を作る作業にスムーズに入ることができました。この作業を子どもの自発的な活動にしたいときには、①で5の缶詰タイルを2、3個入れておくことが生きてきます。
　10を一つ作って、高さをあわせたものをどんどん作れば楽なことに気づかせていきます。この段階ではまだ位取りまでは入りません。もちろん数字も使いません。「たくさんのタイルがあるときには10のタイルを作る」「10のタイルは1本、2本と数える」ことを約束とします。このあと、子どもたちと本のタイル（10のタイル）作りをしました。このなかで、本のタイルはいろいろな作り方ができることを学んでいきました。
　　　　5の缶詰タイル2個で作る
　　　　5の缶詰タイルとバラの5個
　　　　バラタイル10個
で作ることができましたが、10個になったらガムテープでくるんでしまうので、できあがったのは全部同じく「本」のタイルとよびました。

位取り表記と三者関係

　三者関係というのは、

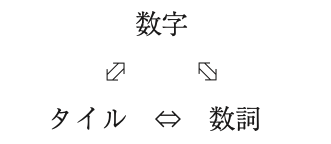
の関係がわかるようになることを指します。
2位数の学習になったら具体物は出しません。具体物では、10ずつが1パックになっているものはタマゴやキャラメルなどいくつかありますが、5・2進になっているものはほとんどありません。操作の観点で見ると具体操作、タイル操作、数の操作（筆算）が一致するものはありません。
　ですから、ここからは「タイル操作」と数の操作である「筆算」を一致させるための学習に入っていきます。
　何度も触れてきましたが「5・2進法」と「10の補数」ではタイル操作が違うということです。子どもはすぐに「5・2進法」の頭になりますから、大人も早く切り替えましょう。わたしは30年以上「5・2進法」で教えているので、逆に「10の補数」は少し考えないと出てきません。

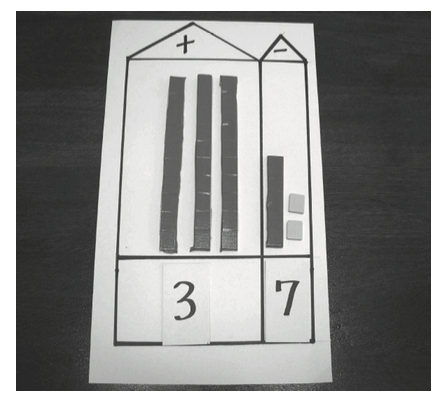
位取り表（十の部屋、一の部屋）を使う

　2桁の数の概念づくりです。2桁の数を言われたときに、タイルと数字が一緒にイメージできるのがねらいです。数詞を書くことは子どもたちには苦手なことなので、読めれば（言うことができれば）いいということにしました。
　タイルを見て→数字カード、数字を見て→タイルを置いて、いくつなのかを言う学習です。
　用意するものは位取り表です。十の位と一の位をそれぞれ部屋に見たてたもので、わたしは厚紙で作りました。タイルと数字カード（1〜9を2組と0を1枚用意）をこの上に置いて使います。

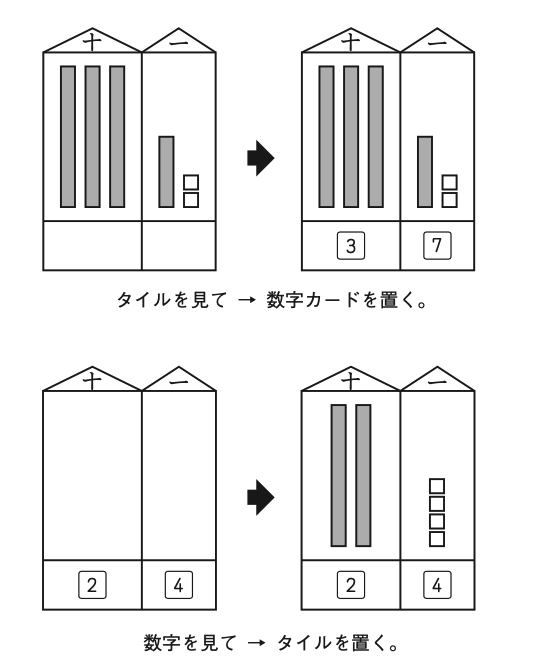
　この枠とタイル、数字カードを使っていろいろな2位数のタイル、数字、数詞のそれぞれの関係がわかること（三者関係）をしました。
　具体物は使いませんが、数を提示するときには、
「○○がサンジュウナナ個」
というように具体的なものの数をイメージさせました。
　あるていどできるようになり、10台の数も読み書きできるようになったところで、次のたし算の学習に進みました。2桁同士の計算のなかで、タイルについてはより習熟していくと考えたからです。
　特別支援学級等で子どもが一人とか二人の場合には、このようにタイルを置きながらの学習ができますが、人数が多いときには巻末添付のプリントをお使いください。

出典：芳賀雅尋『特別支援 99までのたし算・ひき算』2010年、太郎次郎社エディタス